Fun with LinkedIn Queens and Constraints

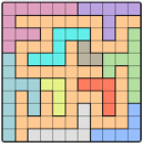I’ve enjoyed solving the LinkedIn Queens puzzle most mornings since they introduced it earlier this year. The problem requires the player to place the queens on a board according to a very brief set of constraints (or rules). For a bit of fun, I wanted to solve the puzzle automatically (or as close as possible) using constraint programming.

Here’s a very rough screencast of the resulting program, which takes a screenshot of the board, figures out the colours in order to formulate a constraint satisfaction problem (CSP), then solves it:

How Does it Work?

Let’s look at this backwards. Once we have a particular problem definition, it’s really simple to solve it using a constraint solver. The problem can be defined in a constraint modelling language.

Modelling the Problem

There are many ways to describe (or model) this problem. The problem states that n queens should be placed on an n by n board so that no two queens are in the same row, column, or are immediately adjacent diagonally. Here’s a constraint model written in Essence Prime:

$ how big is the board?
given n : int

$ define the domain of the decision variables
letting N be domain int(1..n)

$ what is the colour of each square?
given board : matrix indexed by [N,N] of int(0..n-1)

$ in the solution queens are represented by a column id per row
find q : matrix indexed by [N] of N

$ now we define our constraints
such that

$ each queen has to be in a separate column
alldifferent(q),

$ can't be diagonally adjacent
forall r : int(1..n-1) . |q[r] - q[r+1]| > 1,

$ one queen per colour
forall r1 : int(1..n-1) .
  forall r2 : int(r1+1..n) .
    board[r1,q[r1]] != board[r2,q[r2]]

The model above describes the entire class of LI Queens puzzles. In order to solve one particular instance, we need to supply the parameters. Here’s an Essence Prime parameter file for the board shown at the top of the post - each colour is represented by a different number (0-10 for 11 colours).

letting n = 11
letting board=[
[6,  6,  6,  6,  6,  6,  5,  5,  5,  5,  5], 
[6, 10, 10, 10, 10, 10, 10, 10,  5, 10, 10], 
[6,  6,  6, 10,  0,  0,  0, 10,  5, 10,  3], 
[6, 10, 10, 10,  0, 10,  4, 10, 10, 10,  3], 
[2, 10,  0,  0,  0, 10,  4,  4,  3,  3,  3], 
[2, 10, 10, 10, 10, 10, 10, 10,  3, 10,  3], 
[2,  2,  2,  8,  8, 10,  9,  9,  9, 10,  3], 
[2, 10,  2, 10,  8, 10, 10, 10,  9, 10,  3],  
[2, 10,  2, 10,  8, 10,  7, 10,  9, 10,  1], 
[2, 10, 10, 10, 10, 10,  7, 10, 10, 10,  1], 
[2, 10,  7,  7,  7,  7,  7,  1,  1,  1,  1]
]

Solving the problem is as simple as running a constraint solver, such as Savile Row, with the model and parameter files:

savilerow -run-solver li-queens.eprime board.param

We get a solution file which contains the assignment of a queen’s column for each row:

letting q be [8, 1, 5, 7, 10, 2, 4, 9, 3, 11, 6]

Extracting the Problem from a Screenshot

In order to define a game board, we essentially need to work out the dimensions of the board and the colour of each cell. There are many ways to try to do this (some interesting ML approaches will exist), but I came up with the following method, given in python-ish pseudocode below, which tries to figure out the actual colours used in the puzzle, and hence the size of the board (each queen occupies a different colour zone, so the number of colours equals the width of the board).

def learnPalette(image, n_starts, n_neighb, dist_neighb, same_col_threshold):
    """Find the unique game colours from an image of a board"""
    keep = set()
    for _ in range(n_starts):
        homepix = select_random_starting_pixel(image)
        homecol = colour_at(homepix)
        if close_to_black_or_white(homecol): # this is either a gridline or the white border
            continue # to next iteration, choosing a different starting pixel
        good = True
        for _ in range(n_neighb):
            newpix = select_random_neighbour(image, homepix, dist_neighb)
            newcol = colour_at(newpix)
            if newcol != homecol:
                good = False
                break
        if good: # all neighbours had the same colour
            keep.add(homecol)
    # mark as a duplicate any colour which is close enough to another colour
    dupes = set()
    for (col_a, col_b) in keep.combinations(n=2):
        if nearly_same(col_a, col_b, same_col_threshold):
            dupes.add(col_b)
    return keep - dupes

And that’s it. If you want the full details I have the complete code in github - the repository has both the essence prime files and an implementation which uses Google’s OR-tools because the latter is easier to install into a python notebook, although the modelling is less reader-friendly.

Why this post?

I believe that constraint programming and related search and optimisation techniques are an untapped tool that many organisations are unaware of. The big players use them all over the place, e.g. in working out your best route on a map app, or working out compatible dependencies in a software package manager.

For more information, check out:

• CSP Lib, a library of constraint satisfaction and optimisation problems from a variety of fields
• Coursera Course on Discrete Optimisation, an excellent introduction to various optimisation approaches, including constraint programming, local search and mixed integer linear programming
• OR-tools, Google’s suite of optimisation solutions.